Determine prominent colors in a picture, your first AWS Lambda in Go

Hint

This article is part 1 of the series on AWS Lambda. Check out the other articles:

Part 2: Integration testing for AWS Lambda in Go with Docker-compose
Part 3: AWS Lambda CI with Buddy

In this article, we will learn how to write and deploy a Lambda function on AWS Cloud by using Go.

More specifically, we will build a lambda function to process images saved into an S3 bucket and determine the most significative (prominent) colors. These colors are then stored on the bucket object as tags.

This can be very useful to build services where it's useful to catalogue or search images by significative colors.

In this picture you can see a more detailed overview of the data flow for this project:

Image loading...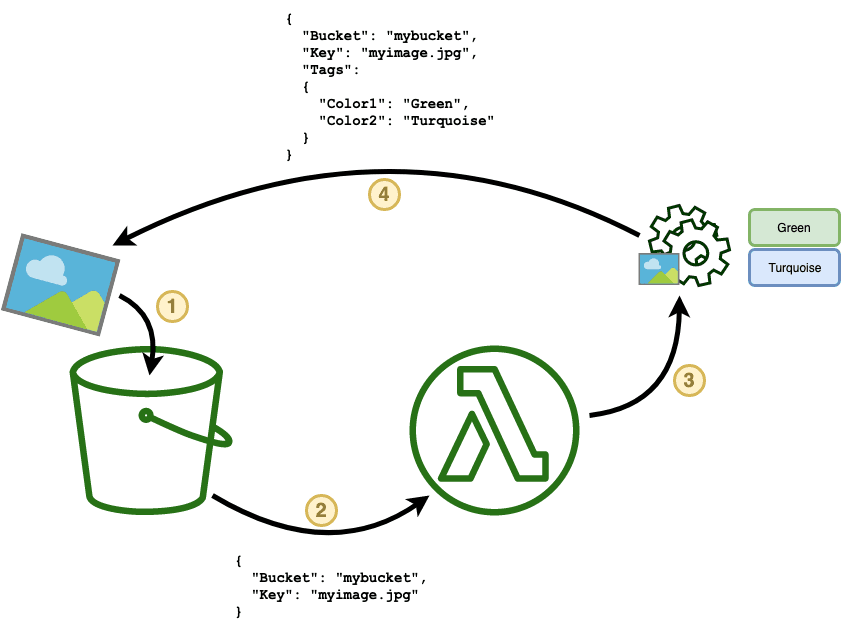

Let's analyse together the different steps:

This is the starting point of the flow: a new image dropped into an S3 bucket will trigger the execution.
The lambda is executed by the AWS engine, which will create an event object that contains all relevant information about the new S3 object to process. This event is passed to the lambda function as an input (more on this later).
The lambda takes the event and uses it to retrieve the content of the new image, reading it from S3 using the AWS SDK. Once the content of the image is loaded, it is processed through a library that allows us to extrapolate a number of the most prominent colors. In this example, the algorithm picked Green and Turquoise as the most prevalent colors of the picture.
At this point, the determined prevalent colors are saved back into the picture object as S3 tags. This operation is done through the AWS SDK as well.

What is a Lambda

If you are here, you probably know already about AWS Lambda and, if that's the case, you should be ok to skip this section.

For those who are new to the concept, Lambda is essentially a cloud runtime that allows you to run code without having to manage servers, this is why Lambda and similar technologies are often referred to as Serverless runtimes.

In the last few years, this approach is gaining a lot of popularity because it offers several advantages over traditional cloud development alternatives:

You don't have to worry about servers, like which operative system to install, when to update, disk space, networking, system optimisations, etc.
Your functions will scale up and down automatically. If you suddenly have a spike of requests, the runtime will automatically allocate more instances of your lambda and distribute the load between them for you. Once the traffic drops, instances are removed to adjust to the decreased load.
You only pay for the amount of computation as a function of the total time taken by all running lambdas and the memory allocated for every execution.
Other important aspects like metrics or logging are provided to you as integration with other cloud services, so again, you don't have to figure out on your own how to support these capabilities.
Finally, as a result of all the above points, you, as a developer, can focus a lot more on the business logic and the value proposition of your product, rather than thinking about infrastructure.

Pre-requisites

Before getting started, let's make sure you have everything setup:

An AWS account (free tier is ok)
AWS command line installed and authenticated
A recent version of Go (1.12 or newer) installed in your development system
Terraform for the deployment

I am also going to assume you have some level of confidence with Go, or that at least you are able to read and understand some simple Go snippets. If you never looked into Go before, you can probably fill the gap by playing a bit with A tour of Go.

Development

All the code that we are going to see today is already available on GitHub for your convenience.

Open or clone the repository called lmammino/lambda-image-colors and let's start by discussing the project structure.

Project structure

In the main folder, we have a Makefile (that will help us to build the final artefact that we will need to submit to AWS) and a go.mod file used to specify the dependencies.

We will be using the following libraries:

EdlinOrg/prominentcolor: a package that allows you to find K prominent colors in an image
jkl1337/go-chromath: color conversion library
aws/aws-sdk-go: AWS Go SDK (for interacting with S3)
aws/aws-lambda-go: tools to develop lambda functions in Go

The main code for the lambda is saved in cmd/image-colors-lambda/main.go and we also have a dedicated file with some utility functions in cmd/utils/utils.go.

Let's start with this utility file.

Utility

This internal utility package will contain the logic that is needed to extract prominent colors and to normalize them to a palette of pre-defined colors.

We can define a palette of colors as follows:

go
type Palette map[string][]uint32

samplePalette := Palette{
  "yellow": {255, 255, 0},
  "pink":   {255, 0, 255},
}

Palette is a custom type that is essentially an alias for a map that relates a string (color name) to an array of integers (the R, G and B components of the color).

The goal of our utils package is to encapsulate all the color extraction logic into a function that will look like this:

go
func GetProminentColors(imageContent io.Reader, palette Palette) ([]string, error) {
  // ...
}

We pass a io.Reader (image content) and a palette of colors and we receive back an array of strings representing the most prominent colors, normalized to the specified palette.

Notice that taking a io.Reader as input is something very convenient, as this abstraction allows us to get the content of the image from different sources: a file from the local file system, the standard input or a file from S3.

Let's get our hands dirty and let's start to implement this:

go
// cmd/utils/utils.go

package utils

import (
  "github.com/EdlinOrg/prominentcolor"
  chromath "github.com/jkl1337/go-chromath"
  "github.com/jkl1337/go-chromath/deltae"
  "math"

  "image"
  _ "image/jpeg" // enables decoding of jpegs
  "io"
)

type Palette map[string][]uint32

func GetProminentColors(imageContent io.Reader, palette Palette) ([]string, error) {
  // 1 - image decoding
  img, _, err := image.Decode(imageContent)
  if err != nil {
    return nil, err
  }

  // 2 - prominent colors extraction
  res, err := prominentcolor.Kmeans(img)
  if err != nil {
    return nil, err
  }

  // 3 - normalize colors to palette
  colors := []string{}
  for _, match := range res {
    colors = appendIfMissing(colors, getClosestColorName(match.Color, palette))
  }

  // return colors
  return colors, nil
}

Let's see what's happening here step by step:

The first thing that we do is to decode the image by using the native Decode function from the image package.
This function converts binary data coming through the io.Reader instance into an Image, which is essentially a matrix of colors (type color.Color). Notice that this function will be able to decode only JPGs because we only imported the image/jpeg package (you can also import image/png and image/gif if you want to support those file types as well).
As per common Go best practices, we also handle the error and we return early if there's an issue with the decoding. We will do this all the time, so from now on I will avoid spending to much time describing error handling.
Here we use the prominentcolor package to extrapolate the colors from the decoded image. The algorithm used here is called Kmeans++ and by default will return a maximum of 3 colors. Colors are returned as a slice of prominentcolor.ColorItem. Every ColorItem is a struct that contains two properties: Color (type prominent.ColorRGB) and Cnt (type int) which is the number of pixels found for that color. We are not really using Cnt in this implementation, but it could be very useful in more advanced implementations where you might be interested in recording the proportion of the different prominent colors.
In this step, we iterate over all the returned ColorItem elements.
For every color we get the closest color to the ones available in the given palette. The resulting color is added to a slice of colors, making sure there are no duplicates.
Here we are using two custom functions appendIfMissing and getClosestColorName, which we still have to implement within our utils package.
Let's start by implementing appendIfMissing:

go
func appendIfMissing(slice []string, value string) []string {
  for _, ele := range slice {
    if ele == value {
      return slice
    }
  }
  return append(slice, value)
}

This function is very simple and pretty self-descriptive, it allows us to append an element to a slice of strings, only if this element is not already present in the slice. With this function, we can essentially guarantee that every color is reported only once from GetProminentColors.

If you are a performance lover, you are probably thinking that you can implement this function in a more efficient way by using hash tables or sets. Keep into account that here we always deal with a very small number of colors (given that our palette is small), so, since the performance difference would be barely noticeable in this case, I preferred simplicity over performance.

Let's now have a look at the implementation of getClosestColorName:

go
func getClosestColorName(color prominentcolor.ColorRGB, p Palette) string {
  minDiff := math.MaxFloat64
  minColor := ""

  // 1 - convert current color to Lab
  colorLab := rgb2lab(color.R, color.G, color.B)

  // 2 - find the closest color in our palette
  for colorName, color := range p {
    currLab := rgb2lab(color[0], color[1], color[2])
    currDiff := deltae.CIE2000(colorLab, currLab, &deltae.KLChDefault)

    if currDiff < minDiff {
      minDiff = currDiff
      minColor = colorName
    }
  }

  return minColor
}

// Utility function that converts a color from the RGB color space to Lab
func rgb2lab(r, g, b uint32) chromath.Lab {
  src := chromath.RGB{float64(r), float64(g), float64(b)}

  targetIlluminant := &chromath.IlluminantRefD50
  rgb2xyz := chromath.NewRGBTransformer(&chromath.SpaceSRGB, &chromath.AdaptationBradford, targetIlluminant, &chromath.Scaler8bClamping, 1.0, nil)
  lab2xyz := chromath.NewLabTransformer(targetIlluminant)

  colorXyz := rgb2xyz.Convert(src)
  colorLab := lab2xyz.Invert(colorXyz)

  return colorLab
}

In order to understand fully this implementation, let me tell you something very quickly about the Lab color space. Actually, let me quote Wikipedia first:

The CIELAB color space (also known as "Lab") [...] expresses a color as three values: L for the lightness from black (0) to white (100), a from green (-) to red (+), and b from blue (-) to yellow (+). CIELAB was designed so that the same amount of numerical change in these values corresponds to roughly the same amount of visually perceived change.

In practical terms, when you want to compare colors (in our case to find the closest color in a given palette), it is very convenient to use the Lab color space, as you can calculate the delta between colors. A small delta means that the two colors are perceived as very similar to human eyes. For instance, two shades of dark red will have a very small delta, while green and blue will have a bigger delta.

There are different algorithms to calculate the delta between two colors in the Lab color space, we are using here the CIE2000. If you are curious to know more about the maths behind this I can recommend you a great article by Zachary Schuessler: "Delta E 101".

With some level of understanding of Lab and CIE2000, the code above should be now quite clear.

Our function getClosestColorName takes a given color in RGB and a palette of RGB colors. The given color is converted to Lab and then compared to all the colors in the palette (in turns converted to Lab as well). The name of the color from the palette with the lower delta will be returned. We also have above a custom function called rgb2lab that is used to perform the conversion. Again there's a lot of color theory around color space conversion and turns out that converting RGB to Lab is not super straightforward. You don't have to understand all the details, but if you are curious you can have a look at this Quora conversation: "What is the equation to convert RGB to Lab? ".

Finally, in our utils package, it is useful to add a function that allows us to instantiate a default palette:

go
func GetDefaultPalette() *Palette {
  return &Palette{
    "red":       {255, 0, 0},
    "orange":    {255, 165, 0},
    "yellow":    {255, 255, 0},
    "green":     {0, 255, 0},
    "turquoise": {0, 222, 222},
    "blue":      {0, 0, 255},
    "violet":    {128, 0, 255},
    "pink":      {255, 0, 255},
    "brown":     {160, 82, 45},
    "black":     {0, 0, 0},
    "white":     {255, 255, 255},
  }
}

Feel free to change this palette if you wish to use different colors :)

CLI

We have been writing a significative amount of code already, and we didn't even start to work on our lambda.

I like to get early results, so, if you are like me, you are probably already thinking about how can you validate what we have written so far before starting to write our lambda...

One way we can do that is by writing a simple CLI app that allows us to pass one or more images and print the prominent colors for every one of them.

Let's do it!

go
// cmd/image-colors-cli/main.go
package main

import (
  "fmt"
  "os"

  // import utils package
  "github.com/lmammino/lambda-image-colors/cmd/utils"
)

func main() {
  // 1 - loads default palette
  palette := utils.GetDefaultPalette()

  // 2 - for every filename passed as CLI argument
  for _, filename := range os.Args[1:] {
    // 3 - open the file
    file, err := os.Open(filename)
    if err != nil {
      fmt.Fprintf(os.Stderr, "Error while opening %s: %s\n", filename, err.Error())
      os.Exit(1)
    }

    defer file.Close()

    // 4 - get prominent colors for the current image
    colors, err := utils.GetProminentColors(file, *palette)
    if err != nil {
      fmt.Fprintf(os.Stderr, "Error while extrapolating prominent colors from %s: %s\n", filename, err.Error())
      os.Exit(1)
    }

    // 5 - print the filename and the prominent colors
    fmt.Printf("%s: %v\n", filename, colors)
  }
}

I added some comments on the main blocks of code to make it easy to understand what's going on here.

One important detail is that we are importing our util package as github.com/lmammino/lambda-image-colors/cmd/utils. We are using an absolute import rather than a relative one. When using Go, it is considered a best practice to always use absolute paths. To make this work with Go module system make sure that your go.mod file contains the following string in the first line:

bash
module github.com/lmammino/lambda-image-colors$

You can generate your go.mod file with the following command:

bash
go mod init github.com/lmammino/lambda-image-colors$

You are free to change the module name, but make sure that you change all the imports accordingly.

In order to populate your go.mod file with all the needed dependencies you can run:

bash
go mod tidy$

And to fetch locally all the dependencies (in a vendor folder) you can run:

bash
go mod vendor$

Let's now run this command line with a sample picture from Unsplash.

bash
go run cmd/image-colors-cli/main.go <path-to-image>$

Image loading...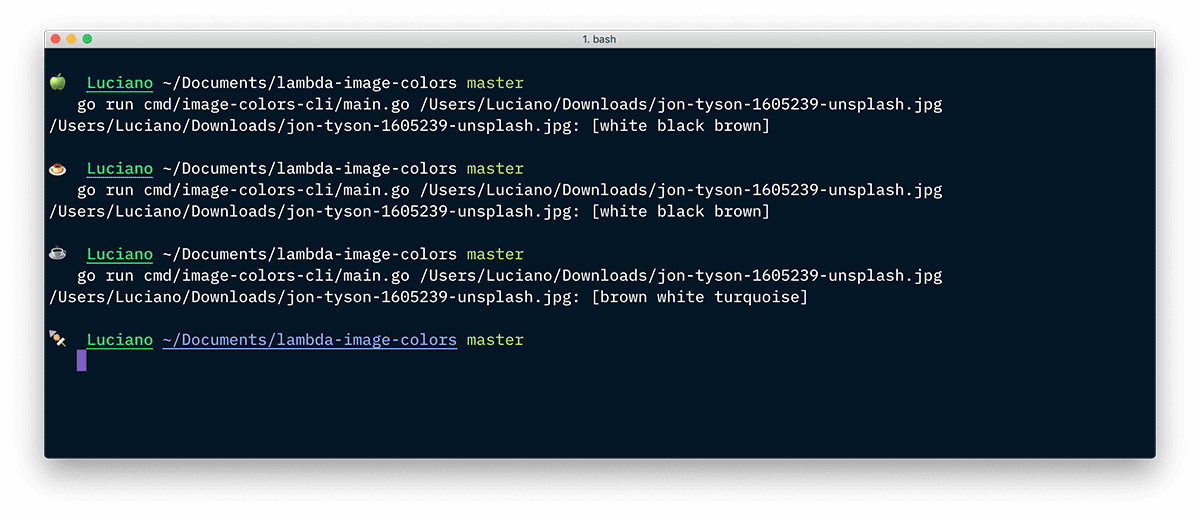

You might have noticed that I am running here the CLI command against the same image three times and that the third time I get a slightly different result. The first and second time we get the colors [white black brown], while the third time we get [brown white turquoise]. If you run the same command on the same image, you will be likely to get different results as well.

This happens because the Kmeans++ algorithm used by the prominentcolor package is not deterministic. Every time you execute it, it might end up aggregating points in a slightly different way and that might affect the way prominent colors are detected.

Ok, now that we know that our library code is reliable let's use it to create a lambda function.

Lambda

Let's finally get to the meat of this article, let's write our Lambda function!

We already described what a lambda is in the first section of this article. Let's see now what is the common signature of a Lambda in AWS when using Go as a language of choice:

go
import "github.com/aws/aws-lambda-go/lambda"

func HandleRequest(ctx context.Context, event SomeEventType) (SomeOutputType, error) {
  // ... your business logic here
}

func main() {
  // start the lambda
  lambda.Start(HandleRequest)
}

A lambda is nothing else but a function that receives some input and it can return some output or an error.

The input comes in the form of an execution context and an event.

The execution context is an instance of the Go Context interface that provides methods and properties with information about the current invocation, the Lambda definition, and other relevant information about the execution environment. For instance, you can use the context to read the current function name, the function version or to call methods like Deadline, which returns the date that the execution times out, in Unix time milliseconds.

The event is generally a struct (or a string) that allows you to pass external information within your lambda. You can use custom events, but most often you will be using Lambda to handle events triggered by other AWS services. In our current example, we want to react to an S3 event.

AWS events have a well-defined structure of fields and types and you can use the aws/aws-lambda-go/events package to import them as structs into your code. For instance, we will be using the S3Event.

Regarding the return types, you can return any data type (as long as it is serializable to JSON). A return type is not mandatory. If you Lambda is not producing any output, you can skip the return type.

Providing an error as a possible return value is not mandatory as well, but I personally advise to always include the error return type (and, of course, to handle errors properly). If an error happens and you return it, the current Lambda execution will be stopped and the failure reported to the AWS metrics system (CloudWatch). In some cases, the Lambda engine will retry failed executions for you.

Given a generic TIn for an input type and a generic TOut for an output type, these are all the supported signatures you can use for writing a Lambda handler function:

func ()
func () error
func (TIn), error
func () (TOut, error)
func (context.Context) error
func (context.Context, TIn) error
func (context.Context) (TOut, error)
func (context.Context, TIn) (TOut, error)

Finally, we have to register our handler. This is done by calling lambda.Start(HandleRequest) in the main function.

This is probably enough context for now, but if you want to know more you can find more details and examples in the official Go programming documentation for AWS Lambda.

Let's see the code for our Lambda function:

go
// cmd/image-colors-lambda/main.go

package main

import (
    "context"
    "fmt"
    "os"

    "github.com/aws/aws-lambda-go/events"
    "github.com/aws/aws-lambda-go/lambda"
    "github.com/aws/aws-sdk-go/aws"
    "github.com/aws/aws-sdk-go/aws/session"
    "github.com/aws/aws-sdk-go/service/s3"
    "github.com/lmammino/lambda-image-colors/cmd/utils"
)

func HandleRequest(ctx context.Context, event events.S3Event) error {
  // 1 - load default palette and initialize a new AWS session and an S3 client
  palette := utils.GetDefaultPalette()
  awsSession := session.New()
  s3Client := s3.New(awsSession)

  // 2 - an S3 event can contain multiple events (multiple files)
  for _, s3record := range event.Records {
    // 3 - load the current file from S3
    bucket := s3record.S3.Bucket.Name
    key := s3record.S3.Object.Key
    s3GetObjectInput := &s3.GetObjectInput{
      Bucket: &bucket,
      Key:    &key,
    }
    s3File, err := s3Client.GetObject(s3GetObjectInput)
    if err != nil {
      return err
    }

    // 4 - calculate the prominent colors of the image
    colors, err := utils.GetProminentColors(s3File.Body, *palette)
    if err != nil {
      return err
    }
    fmt.Printf("Indexing s3://%s/%s with colors -> %v\n", bucket, key, colors)

    // 5 - Attach multiple tags ("Color1", "Color2", "Color3") on the S3 object
    tags := []*s3.Tag{}
    for i, color := range colors {
      tagKey := fmt.Sprintf("Color%d", i+1)
      tag := s3.Tag{Key: aws.String(tagKey), Value: aws.String(color)}
      tags = append(tags, &tag)
    }
    taggingRequest := &s3.PutObjectTaggingInput{
      Bucket: &bucket,
      Key:    &key,
      Tagging: &s3.Tagging{
        TagSet: tags,
      },
    }
    _, err = s3Client.PutObjectTagging(taggingRequest)
    if err != nil {
      return err
    }
  }

  // 6 - No error, completed with success
  return nil
}

func main() {
    lambda.Start(HandleRequest)
}

This code is unsurprisingly similar to the CLI tool we wrote previously, we are just replacing filesystem operation with AWS S3 operations. Let's review together all the important steps:

At the very beginning of our handler, we load the default palette and we create an instance of an S3 client using the AWS SDK. It's ok to use the default settings for the S3 client, this way the client will automatically use the current region (where the Lambda is deployed) and the role attached to the Lambda (more on this later).
Since an AWS S3 event can contain multiple records (multiple images) we have to iterate over all of them.
Inside the loop, we load the content of the S3 object by using our instance of the S3 client. s3File.Body implements io.Reader to allow us to consume the raw bytes of the image saved in S3.
We use utils.GetProminentColors to get the prominent colors of the current image and we print the result. Everything we print within a Lambda will be streamed to a Cloudwatch log stream, which we can observe to make sure our lambda is working as expected.
Finally, we need to create the tagging request to attach tags to the original S3 object. Here we iterate over the prominent colors and create a list of s3.Tag items. The name of every tag has the form Color%d, where %d is a number from 1 to 3 (since we return a maximum of 3 prominent colors from our utility function).
If we reach the end of the handler it means everything went smoothly and we can return nil which indicates there was no error.

Infrastructure and deployment

Now that our code is ready, you are probably wondering how do we deploy our Lambda to AWS.

In my opinion, this is the least friendly part of Serverless. So far everything was quite easy and enjoyable and we really focused only on defining the business logic of our Serverless application.

Of course, Serverless is not magic! We still need to define the necessary configuration for our Lambda: runtime details like allocated memory and timeout, AWS permissions, event triggers, etc. We also have to compile and package our code as expected by the Lambda runtime.

This is when having proper tools and automation in place is going to make our life easier and still allow us to focus most of our time on business logic rather than on infrastructure.

Packaging

Let's see how to package our new Lambda application. In order to run code written in Go in Lambda we have to compile it for Linux. The resulting binary must also be compressed using zip.

We can add the following entry to our Makefile in order to build the lambda code and create a proper artefact in build/image-colors.zip.

makefile
.PHONY: build
build:
    go mod tidy
    go mod vendor
    mkdir -p build
    GOOS=linux go build -mod=vendor -o build/image-colors ./cmd/image-colors-lambda
    cd build && zip image-colors.zip ./image-colors
    echo "build/image-colors.zip created"

Notice that we are always running go mod tidy and go mod vendor, to make sure that our dependencies are in check before we build.

With this in place, we just need to run:

bash
make build$

And we should obtain the expected artefact in the build folder, ready to be uploaded to AWS.

Permissions

Yeah... policies, roles etc! In my opinion, these are probably the best and at the same time the most annoying AWS features. If you have been working with AWS long enough, I am sure you know what I mean by that. If you haven't, let me just say that AWS has a very granular and powerful security model through policies. This model allows you to build applications that get only the very minimum level of permissions needed to perform their task. This is a fantastic security best practice, but sometimes it is a bit tricky to configure permissions properly and you will end up with having to try multiple configurations until you get the right one. In any case, this is a good exercise and will let you think very carefully about what's important for your application from a security standpoint. So, don't skip it and, please don't just give your application admin access just to avoid the trouble. Sooner or later you will regret that choice!

But enough with the security talk and let's get practical. If we think again about our current use case we essentially want our lambda to be able to perform 2 main actions:

Read the content of objects from a given S3 bucket
Add tags to objects in the same S3 bucket

So we need to make sure our Lambda will have appropriate permissions to perform these actions, otherwise, we will end up with a runtime error for lack of permission.

In reality, there are some more generic permissions that a Lambda (almost) always needs to have:

Ability to assume a role
Ability to create a log stream in Cloudwatch

The first permission essentially means that the lambda can get its own role once executed. In AWS, you can see a role as a container for different policies that can be assigned to a user or a compute resource like a Lambda or a virtual machine. A policy contains multiple statements and every statement is essentially a grant to perform a given action on a given resource.

The ability to create a log stream in Cloudwatch is necessary if you are writing in the standard output. Lambda redirects all output to a stream in Cloudwatch (this is where you can see Lambda logs), so the lambda should be able to perform this operation.

We will be using Terraform to generate all the necessary roles and policies in your AWS account, but if you want to understand this part better (or if you simply want to create everything manually in the AWS web console), here follow some templates for roles and policies.

Lambda role

The lambda role contains the following role policy:

json
{
  "Version": "2012-10-17",
  "Statement": [
    {
      "Action": "sts:AssumeRole",
      "Principal": {
        "Service": "lambda.amazonaws.com"
      },
      "Effect": "Allow"
    }
  ]
}

This essentially says: "This role can be assumed by a Lambda". We will be saving this role as image-colors-lambda (aws_iam_role).

S3 permissions

Now let's create a policy to grant all the permissions needed to interact with S3, we are going to call it image-colors-lambda-s3-access (aws_iam_role_policy):

json
{
  "Version": "2012-10-17",
  "Statement": [
    {
      "Effect": "Allow",
      "Action": [
        "s3:ListBucket"
      ],
      "Resource": [
        "${aws_s3_bucket.images_bucket.arn}"
      ]
    },
    {
      "Effect": "Allow",
      "Action": [
        "s3:GetObject",
        "s3:PutObjectTagging"
      ],
      "Resource": [
        "${aws_s3_bucket.images_bucket.arn}/*"
      ]
    }
  ]
}

We are using a variable here:

aws_s3_bucket.images_bucket.arn: The ARN (unique identifier) of the S3 bucket containing the images we want to process.

This is a Terraform variable. If you are creating the policy manually, make sure you replace it with the actual ARN of your bucket.

As you can easily see, this policy is essentially allowing the bearer to list objects in a given bucket and to get content and add tags on objects in the same S3 bucket.

Cloudwatch permissions

Finally, let's create the necessary policy for Cloudwatch logging which we will call image-colors-lambda-cloudwatch-access (aws_iam_role_policy):

json
{
  "Version": "2012-10-17",
  "Statement": [
    {
      "Effect": "Allow",
      "Action": [
        "logs:CreateLogStream"
      ],
      "Resource": [
        "arn:aws:logs:${data.aws_region.selected.name}:${data.aws_caller_identity.selected.account_id}:log-group:/aws/lambda/image-colors:*"
      ]
    },
    {
      "Effect": "Allow",
      "Action": [
        "logs:PutLogEvents"
      ],
      "Resource": [
        "arn:aws:logs:${data.aws_region.selected.name}:${data.aws_caller_identity.selected.account_id}:log-group:/aws/lambda/image-colors:*:*"
      ]
    }
  ]
}

Here we have some more variables:

data.aws_region.selected.name: the name of the AWS region where the Lambda is deployed.
data.aws_caller_identity.selected.account_id: the current AWS account ID

If you want to create all these policies manually, don't forget to attach them to the Lambda role we defined above.

Lambda configuration

Let's see how to configure our Lambda runtime. Again, this is something that our terraform setup will do for you, but in case you want to try to configure everything manually from the web console, this is what you have to set:

Lambda source code: use the zip file created by our build script in build/image-colors.zip.
Function name: this is the name of the Lambda function, you can use image-colors.
Role: attach the role we defined previously as image-colors-lambda.
Handler: this is the name of the handler function in our Go code, use image-colors.
Runtime: go1.x.
Memory size: how much memory is allocated for every Lambda instance. I tested this code against 256Mb and it was running fine. If you plan to upload very large images you might need more, but take into account that your cost per execution will grow if you allocate more memory.
Timeout: how much time your Lambda function has available before timing out. I set this to 30 seconds, which is generally more than enough with regular images. In this case if you Lambda finishes early you are not charged for the full 30 seconds block, so you might be generous with this setting if in doubt.
Reserved concurrent executions: this setting allows you to limit how many concurrent instances of this Lambda you can have at a given time. Your total number of concurrent Lambda instances (across all functions) is limited by 1000 by default. This means that in a real production scenario you might want to limit how many instances can be allocated for a given Lambda. For instance, if you expect to drop thousands of images in our S3 folder you are definitely better off limiting the number of concurrent executions to avoid this Lambda taking all the available capacity. Our Terraform script will set this value to 10, which should be a good default.

Another thing you have to configure is the Lambda event. Make sure to select the correct bucket and, optionally you can also add a filter suffix to ".jpg" to make sure that the Lambda execution gets triggered only on images.

Deployment

All the Terraform code is available in the stack folder.

I will not go into much details about how this code actually works but I will try to explain at a very high level how to run Terraform and what is going to happen with our current setup. This will probably be enough for you to understand the structure of the code.

Before getting started, open a terminal and move the prompt into the stack folder. Now run the following command to initialize the Terraform environment:

bash
terraform init$

Now, to have a quick idea of what is going to be provisioned in your AWS account with this Terraform setup, you can run the following command:

bash
terraform plan$

If all goes well, you should see a long output representing a preview of all the AWS resources that Terraform will create for you, which should contain the following:

aws_iam_role.image-colors-lambda: the role that we will assign to the Lambda.
aws_iam_role_policy.image-colors-lambda-cloudwatch-access: the policy to grant the Lambda permission to write logs to Cloudwatch.
aws_iam_role_policy.image-colors-lambda-s3-access: the policy to grant the Lambda permission to read from S3 and to add tags to objects.
aws_lambda_function.image-colors: our actual Lambda function.
aws_s3_bucket.images_bucket: the S3 bucket where we will save the images.

Also Terraform will generate a random ID called stack_id which will be used as a suffix for your bucket name as this has to be unique across all the AWS accounts.

By default the current Terraform setup will deploy everything in the us-east-1 region (North Virginia). If you wish to use a different region, make sure to edit that in the main.tf file.

If you want a better understanding of what is happening here, Terraform is essentially figuring out all the dependencies in the resources graph and it builds an internal representation that might look like the following:

Image loading...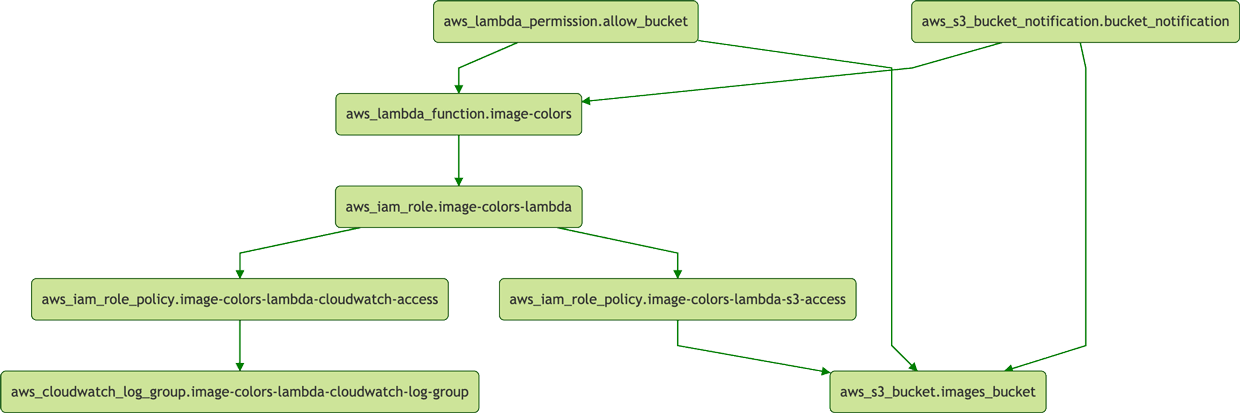

By looking at this graph, Terraform knows which resources should be created first. An arrow indicates that a resource depends on the one that the arrow is pointing to. Here, Terraform should start from any resource at the bottom, because they have no dependency.

Now, to actually apply the changes and deploy the various resources in your account you can run:

bash
terraform apply$

This command should show you a preview of the resources to be provisioned as we saw before, but this time you should also see a prompt that asks you whether you want to proceed with the provisioning or not. Input yes to confirm.

If everything went well you should see something like the following output at the bottom of your screen:

plain
Apply complete! Resources: 7 added, 0 changed, 0 destroyed.

Outputs:

cloudwatch_log_group = arn:aws:logs:us-east-1:012345678901:log-group:/aws/lambda/image-colors
s3_bucket = image-colors-abcdef1234567890abcdef1234567890
stack_id = abcdef1234567890abcdef1234567890

Take note of the Outputs values as we will need them shortly.

Note that Terraform is not the only way to provision Lambda functions on AWS, there's no shortage of alternative solutions. Among the most famous:

CloudFormation: the official solution from AWS for cloud provisioning.
SAM (Serverless Application Model): another solution by AWS, a more expressive dialect of Cloudformation focused on Serverless deployments.
Serverless framework: an open source multi-cloud project focused on deploying Serverless projects.

Testing

Ok, finally everything is in place. Our Lambda and S3 buckets are ready for use to publish some images.

In order to copy images to the S3 bucket, you can run the following command:

bash
aws s3 cp <path-to-local-image> s3://<name-of-s3-bucket>/$

Make sure to replace the values with the correct ones in your system, for instance in my case I can do something like this:

bash
aws s3 cp /Users/Luciano/Downloads/jon-tyson-1605239-unsplash.jpg s3://image-colors-abcdef1234567890abcdef1234567890/$

Once the upload is completed, our Lambda should be triggered.

We can verify if everything worked as expected by having a look at the Cloudwatch logs. This is not super straightforward to do from the command line, so you might prefer to go to the web dashboard instead. If you feel in the mood for some CLI kung fu though here's what we can do to check out our Lambda logs:

bash
aws logs describe-log-streams \
  --log-group-name /aws/lambda/image-colors \
  --region us-east-1 \
  --output text | head -n 1$$$$

This command will describe all the log streams in our log group. A Lambda can generate multiple log streams over time under its own log group, here called /aws/lambda/image-colors. The actual log lines are stored in a log stream.

With this command you should see an output similar to the following:

plain
LOGSTREAMS    arn:aws:logs:us-east-1:012345678901:log-group:/aws/lambda/image-colors:log-stream:2019/04/16/[$LATEST]abcdef1234567890abcdef1234567890 ...

The name of our log stream is the following: 2019/04/16/[$LATEST]abcdef1234567890abcdef1234567890.

Now we can run this command to get the actual log lines:

bash
aws logs get-log-events \
 --log-group-name /aws/lambda/image-colors \
 --log-stream-name '2019/05/27/[$LATEST]abcdef1234567890abcdef1234567890' \
 --region us-east-1 \
 --output text$$$$$

With this command you should see something like this:

plain
EVENTS    1558984276627    START RequestId: 12345678-3679-408d-8202-244a73a04fdc Version: $LATEST
    1558984261545
EVENTS    1558984276627    Indexing s3://image-colors-abcdef1234567890abcdef1234567890/jon-tyson-1605239-unsplash.jpg with colors -> [brown white turquoise]
    1558984265776
EVENTS    1558984276627    END RequestId: 12345678-3679-408d-8202-244a73a04fdc
    1558984265815
EVENTS    1558984276627    REPORT RequestId: 12345678-3679-408d-8202-244a73a04fdc    Duration: 4269.58 ms    Billed Duration: 4300 ms     Memory Size: 256 MB    Max Memory Used: 79 MB

Here you can see that the Lambda produced the expected output:

plain
Indexing s3://image-colors-abcdef1234567890abcdef1234567890/jon-tyson-1605239-unsplash.jpg with colors -> [brown white turquoise]

The colors extracted for our image are brown, white and turquoise.

Notice also that the log displays how much memory was used, how long the execution took and the number of milliseconds that will be accounted for in the Lambda billing.

Let's now verify that the object in S3 has the expected tags:

bash
aws s3api get-object-tagging \
  --bucket image-colors-abcdef1234567890abcdef1234567890 \
  --key jon-tyson-1605239-unsplash.jpg$$$

Which should produce the following JSON output:

json
{
  "TagSet": [
    {
      "Value": "turquoise",
      "Key": "Color3"
    },
    {
      "Value": "white",
      "Key": "Color2"
    },
    {
      "Value": "brown",
      "Key": "Color1"
    }
  ]
}

YAY, if you got a similar result, everything works as expected! Congratulations on running your first Lambda in Go :)

Conclusion

Well, I hope you enjoyed this tutorial and that this is just the first over many Lambda that you will create. Maybe you will even build an entire application adopting the Serverless paradigm.

If you want to clean up everything created by Terraform during this tutorial you can do so by deleting all the files in your S3 bucket and then by running the terraform destroy command (from within the stack folder):

bash
aws s3 rm --recursive s3://image-colors-<your-stack-id>/
terraform destroy$$

If you are looking for new ideas on what to build next, well I can give you a few:

A Slack bot that keeps your colleagues happy by reminding them how many hours are left until the end of the week.
A Lambda that can monitor your favourite products and warns you once the price goes down.
An Alexa skill to book a spot in your local Yoga class.

Until next time, ciao!

PS: A huge thank you goes to my amazing colleague Stefano Abalsamo (@StefanoAbalsamo) for proofreading and testing all the code in this article and to Simone Gentili (@sensorario) for providing a ton of advice on how to make the article better. Simone is also the author of Go Design Patterns, check it out to learn some cool new stuff about Go!

Next in series: Integration testing for AWS Lambda in Go with Docker-compose

Luciano Mammino

Senior Architect @ fourTheorem

Luciano is a FullStack & cloud developer who wrote his first line of code at the age of 12 on his father's old i386. Since then, he has never stopped coding. He is working at FabFitFun as Principal Software Engineer where he is building software to serve millions of users every day. He loves the fullstack web, Node.js & Serverless and co-authored "Node.js design patterns".

Read similar articles

Structural Pattern Matching In Python Why Laravel is the Best PHP Framework In 2021?

Oct 10, 2020

Last update: Feb 8, 2024

On this page

Infrastructure and deployment

Cloudwatch permissions

Determine prominent colors in a picture, your first AWS Lambda in Go

What is a Lambda

Pre-requisites

Development

Project structure

Utility

CLI

Lambda

Infrastructure and deployment

Packaging

Permissions

Lambda role

S3 permissions

Cloudwatch permissions

Lambda configuration

Deployment

Testing

Conclusion

Start for free

Self hosted

Cloud